Calculating Field of View
I have telescopes and camera lenses. At times, I want to know which lens is needed to frame a known subject in the frame. With the telescope, I may want to know how much of a nebula will fit in my field of view. I have even calculated the distance to an elk I imaged with a 400mm telephoto lens on my DSLR. There are ways to calculate these angles.
A lens’s focal length can determine its angle of coverage. The other factor that is needed is the size of the imaging device. A small imager will cover a smaller area while a larger imager will cover a wider area. Sounds obvious but what you may want to know is just how much of the sky or landscape a certain lens will cover with a specific camera. The equation we will be working with is 2 arctan W/f, for the width, 2 arctan H/f, for the height.
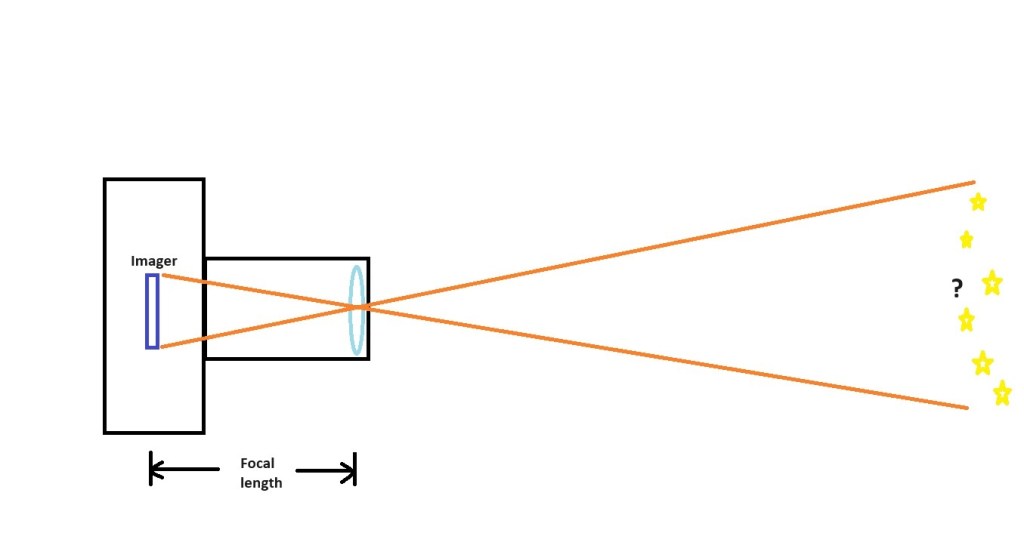
The first thing I check is the imager dimensions. Since I use DSLR’s I will use the dimensions from my Canon 60D and 90D. Their imagers both measures 14.9 x 22.3 mm. Since this ratio is 1.5 to 1, calculating for “Height” or 14.9 in this case, all you need to do is multiply the final “Height” by 1.5 to get the “Width.”
This diagram condenses all the elements we will be covering. Feel free to print it out for reference but it is copyrighted by me so do not post it anywhere else for any reason.
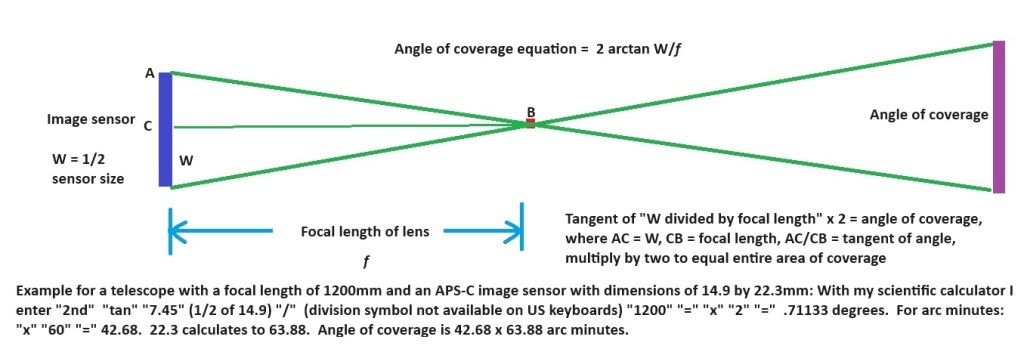
Let me break it down for you. A right triangle is the basis for our calculations. To find the angle of coverage for a lens, we will calculate that angle by dividing the imager dimension by two and when we are done, multiply the result by two to get the final full angle of coverage. In the diagram above, the height of the right triangle is represented by the length AC. The focal length of the lens will be represented by the length BC as in the diagram below.
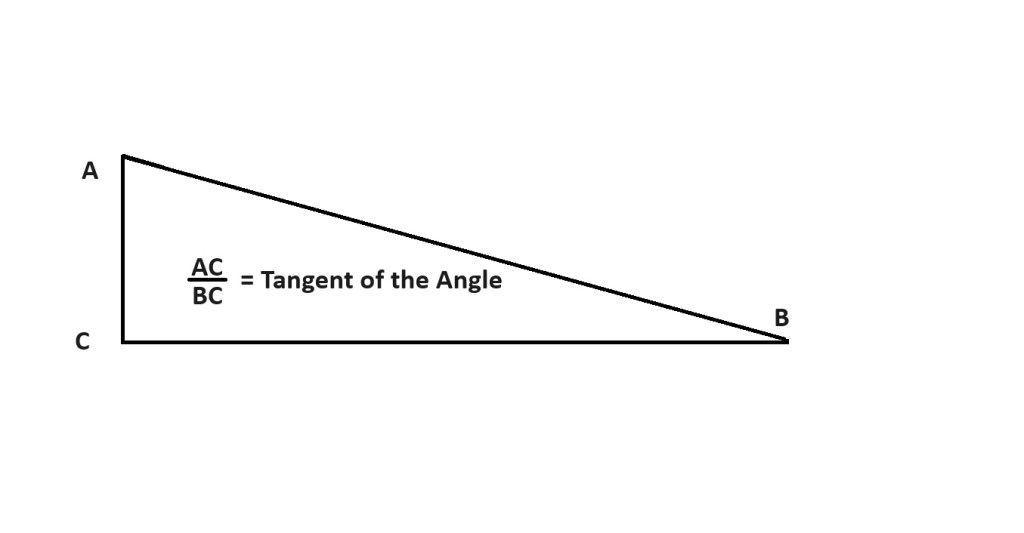
The length AC divided by the length BC equals the tangent of the angle. A table of Tangents can be used to find the resulting angle. Here is an example: Canon 60D imager is 14.9 mm tall. Divide that number by two to get length AC or 7.45 mm. Using the focal length of my ten-inch Newtonian reflector which is 1200mm, we get .006208333. A table of tangents gives us an angle between 21 and 22 arc minutes. Using a calculator, we get .355706728 degrees, which is 21.3424 arc minutes. Now all we need to do is multiply by two to get the final angle covered by the height of this imager. The result is an angle of 42.6848. Multiply by 1.5 and we get the Width coverage, or 64.0272 arc minutes.
On my scientific calculator I enter “2nd” “tangent” “7.45” “/” (divided by) “1200” “=” “x” “2” “=” “.711413456” degrees. “.711413456” “x” “60” “=” “42.68480734” arc minutes.
When I want to take an image of an astronomical object, I plug these figures into my planetary program. It allows me to make a field of view box that I can use to frame my subject. Using the calculations above I made this estimate of how I wanted to frame the Orion Nebula and the resulting image.

Now we will consider a telephoto lens on a 90D that has the same sized imager. If we attach a 200 mm lens, we now divide the 7.45 by 200 to get .03725. The tangent chart lists 2 degrees plus somewhere between 6 and 12 arc minutes. The calculator gives us 2.133281465 degrees (.133281465 degrees equals 7.996887874 arc minutes, thus 2 degrees and about 8 arc minutes). We multiply by two to get the final height or 4.266562929 degrees. Multiply by 1.5 and we get the width of 6.399844394. Our final area of coverage is 4.267 by 6.4 degrees (4 degrees, 16 arc minutes by 6 degrees, 24 arc minutes).
This is an image using that lens.

This is the area shown in my computer’s planetarium program.

Now for a different use. Recently I took a couple of beautiful images of a bull elk jumping a fence. I used the 200 mm lens on a Canon 90D (same sensor dimensions) and a teleconverter for a final focal length of 400 mm.

I wanted to know the distance to the elk. I calculated a field of view of 2.134 by 3.2 degrees. We will use the width dimension but multiply by 60 to get arc minutes (192.0618947). I printed out the image and measured the width of the image on an 8.5 x 11 sheet of paper at 10.625 inches. A full-grown bull elk is very close to four feet from chest to rump. He measures 9/16 (.5625) inch long on that sheet. 10.625 divided by .5625 inches equals 18.89. The elk takes up about 1/19 of the image. The width in arc minutes is 192.0618947, divided by 18.89 equals 10.16798267 arc minutes, making the elk measure about 10 arc minutes across. Now where are we? We now know the angle (10.16798267 arc minutes) and the “width” (4 feet) of that angle, now we need to know the length, just like the focal length. We could go into cotangents but let’s do the simple method. 10.16798267 arc minutes is .169466378 degrees. 360 degrees divided by .169466378 equals 2124.315184, which equals a four-foot length. Multiply by 4 equals a circle of 8,497.260737 feet. Divided by pi (3.141597) equals 2704.762098 feet. Divide by two to get the radius of the circle or 1352.381049 feet. In yards, 450.793683. The distance to the elk was about 450 yards, give or take a couple dozen due to rough estimates on an 8.5 x 11 inch print.
Cropped images of the elk jumping the fence.


In case you are wondering, when I do cross checking using cotangents, I get 1352.377105 feet (450.8 yards). I also found about the same distance when I used a cotangent chart and calculated the approximate figure the chart would have listed. It only lists 6 arc minutes for a factor of 573 and 12 arc minutes at 286.5. If I estimate what the list might be at 10.16798267 arc minutes, it would have listed around 330 to 340 (the calculator says it should be 338.0942763). 4 feet times the 330 equals 1320 feet or 440 yards. 340 equals 453 yards.
I believe they use a similar method to measure the distance to stars. As Earth orbits around the sun, it covers a cross section (diameter of orbit) of about 186 million miles (299.8 million kilometers). Divide by two and you get a baseline (AC above) of 93 and 149.6 million. If the angle is one arc second, what would the distance be? Feel free to do the math but it is a well known fact that it is 3.26 light years (1.917 × 1013 miles or 3.086 × 1013 kilometers). One parallax-second of arc, or parsec for short.