I wanted to know if I could catch the deflection of a star as it passed the gravity well of the sun during the upcoming total eclipse. Zeta Piscium will be less than a degree form the sun as seen from southern Texas. I could assume that it would be extremely difficult since they had such difficulties back in 1919 in trying to prove General Relativity, but I like challenges and math can be fun so I thought I would calculate it myself. To quote a famous line from the movies, “How hard can it be?” Well, hard!
A brief description may be necessary. Einstein posited that gravity must alter the path of a light ray if it passes through a powerful gravity field, also known as a gravity well. The amount of deflection would rely on the intensity of the gravity field. Einstein needed to learn tensors to be able to solve the equations needed. At first I thought I would have to but at least for this, no tensors needed. Actually, I don’t think I would live long enough to understand tensors after I did a quick perusal of the theory! After a few web searches, I finally found the equation for determining the angle of deflection. Whew! Only normal algebra! This is the equation.

The “delts psi” symbols will represent the final angle of deflection in radians. A radian is the angle achieved when the circumference is divided by pi and divided by two. It simplifies calculations when you need the relationship between radius and circumference. A radian is equal to 57.29577951 degrees. ”G” is the gravitational constant. This format does not like exponents so exponents will be written with “^” followed by the exponent, thus four squared will be written as “4^2.” The Gravitational constant is:
6.67430 (+or- .00015) x 10^-11 x m^3 x kg^-1 x s^-2. ”m” = meters, “kg” = kilograms and “s” is seconds.
“M” is the mass of the object deflecting the light path or in our case the Sun. M = 1.9891 x 10^30 kg.
“C” is the speed of light in meters per second or 2.99792 x 10^8 mps.
“d” confused me for a while. I could not find what units it was supposed to be in. Eventually I found that it is the distance in meters from the center of the object (the Sun) at its closest approach in passing. That leaves us with, “what is that distance?” First here is a graphic representation of what is happening.
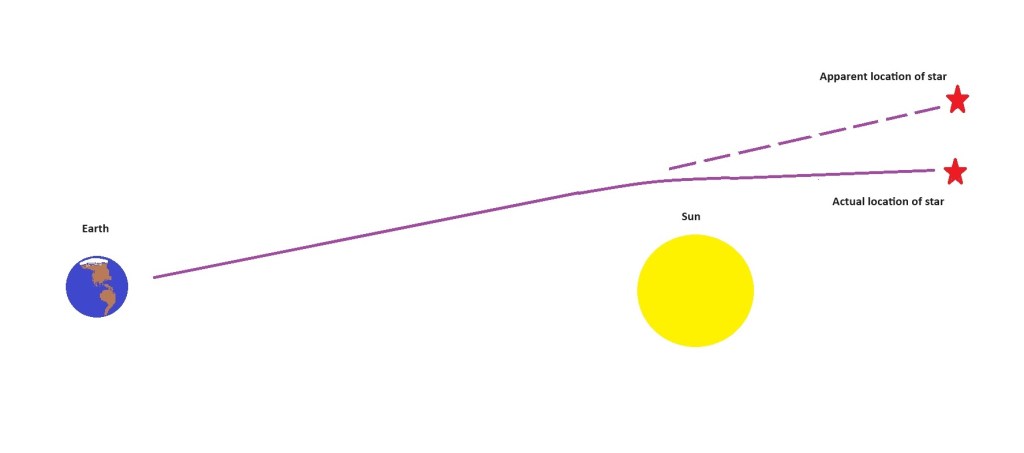
“d” is going to be the distance from the Sun’s center to the line as it passes the Sun. Now I need to know what star will be my target. This image from the planetarium program “The Sky Professional X” shows the area around the eclipse as seen from southern Texas.

The brightest star to the left of the image of the Moon is Zeta Piscium. After calculating its angular distance I found it is about .824 degrees from the center of the image of the Moon (which is covering the image of the Sun). I may be off by an arc minute but close enough for our purposes. I calculated that the angle at our distance would translate to 2.141559833 x 10^9 meters and that will be our “d.” There is no need to be so exact but it adds difficulty (and looks cool).
When I plug these numbers into our equation I get:
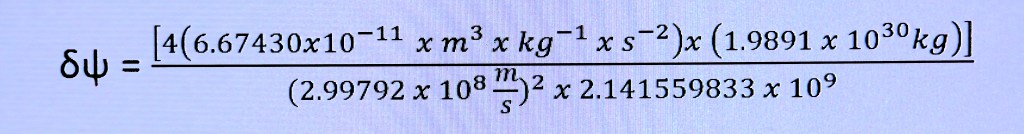
After getting my calculator and reducing to simpler terms I get:
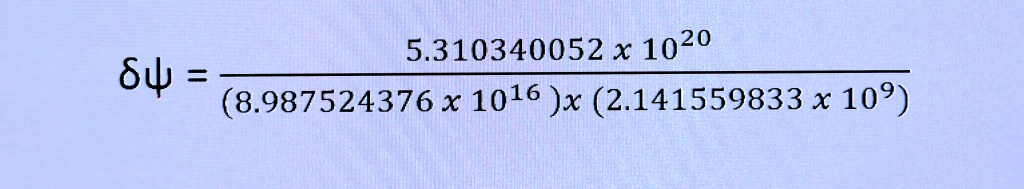
Then:

Which the final result is “Delta Psi” = .000002759 Radians = .568885952 arc seconds.
The resolution of my telescope that I will be using has a Dawes Limit of 1.45 arc seconds which is not sharp enough to see this shift.
But wait! Is my math correct? It took awhile to find what the details of Eddington’s expedition in 1919 was. They calculated that if the star was right at the Sun’s limb, the angle of deflection would be 1.75 arc seconds. I then figured what “d” would be at that time. ”d” is now 6.9635 x 10^8 meters. Here are my results:
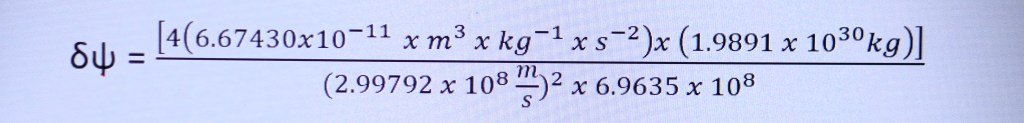
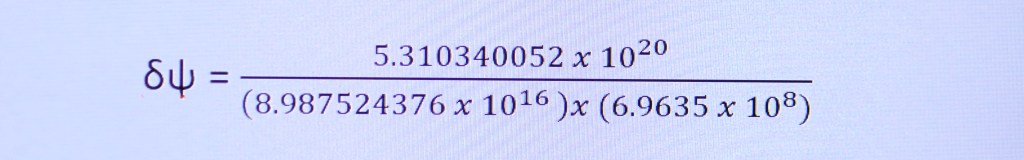

”Delta Psi” is now .000008485 Radians or 1.750168263 arc seconds. Math verified.
Hopefully I did not make any mistakes and achieved the results I did by accident! Feedback is always welcome.
If your telescope will be able to capture the 8.77 magnitude star, SAO 109699, which is just right of the eclipsed Sun (the corona may be too bright), then its light path is only 1.023792435 x 10^9 meters from the center of the Sun. I’ll let you do the math but the deflection will probably be above one arc second. Zeta Piscium is magnitude 6.26 which may be bright enough to show through the corona.
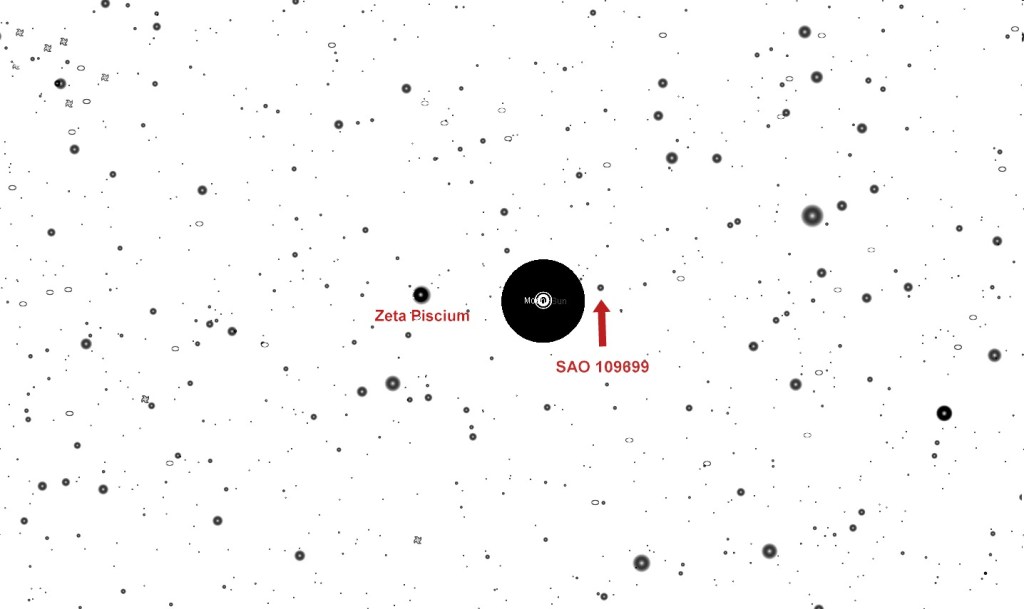
This is a view of the starfield without the Sun and Moon. ISO was 400, focal length 300mm, exposure 1 second at f5.6. The dim star just above center is SAO 109699, Zeta Piscium is the bright star to the left.

That was fun!
BTW. I was clouded out. All I captured was several seconds through dense clouds. I stacked 12 images and got a half decent image (below).

This is how it looked during totality.

This is what each image looked like before stacking and processing (cropped). I saw this for about three seconds or so, tripped the shutters and had to coax the above final image out of twelve RAW images. Then it clouded up for several minutes and then I got a few seconds for imaging just after Baily’s Beads (below). Again it was through dense clouds.

